Cubic Spline Interpolation
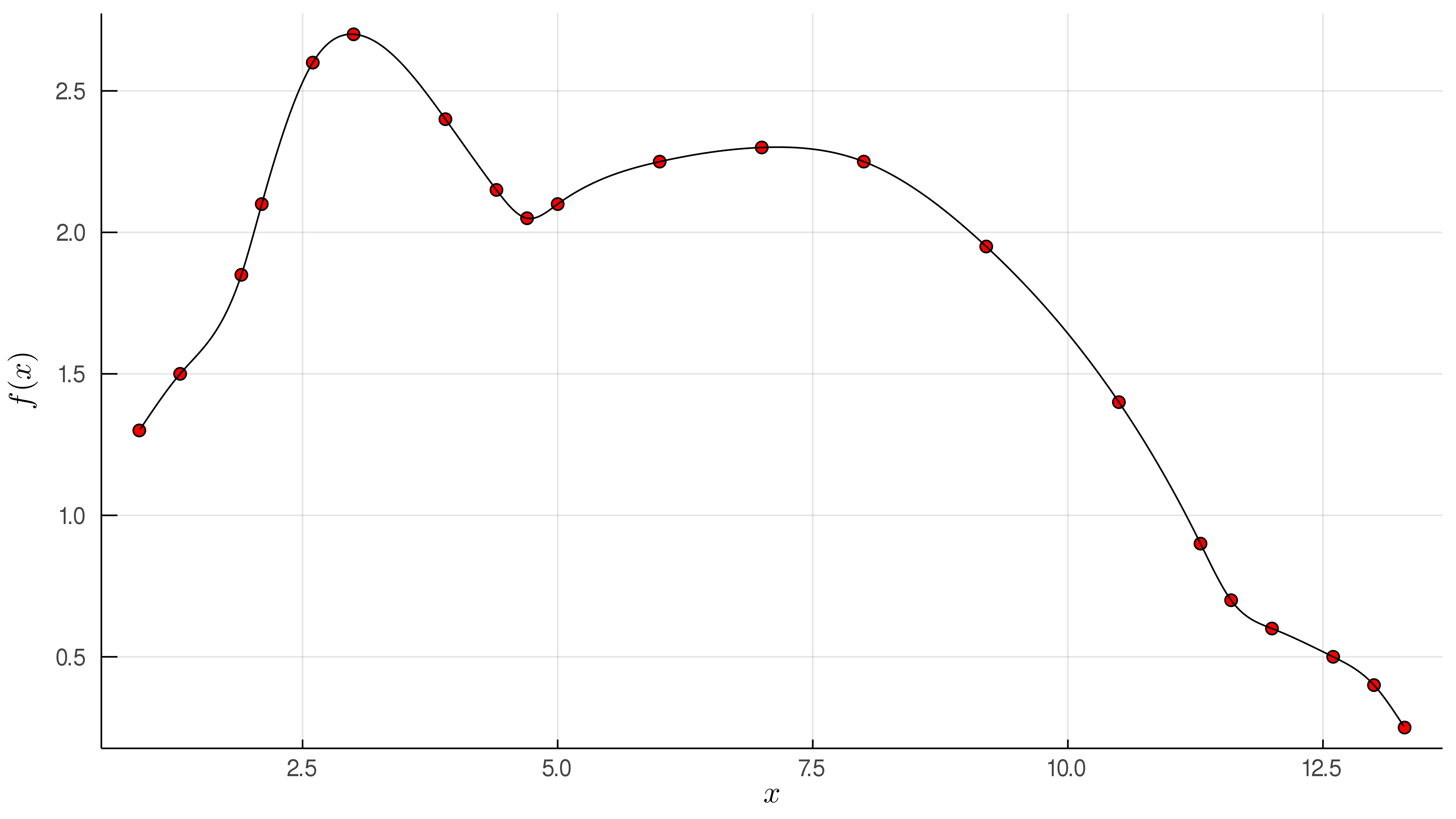
Whenever one has a set of discrete data points given by sampling or experimentation, they correspond to the values of a certain function. Since we don't know the complete set of values, one needs to interpolate in order to estimate the value of the function between the known data. For this, it is required a spline which is functioned defined piecewise by polynomials of order $k \in N$ differentiable $k-1$ times in $[a,b]$: $S(x) \in C^{k-1}[a,b]$.
This spline must satisfy three basic conditions:
1. Continous function: $S_{i-1,i}(x_i) = S_{i,i+1}(x_i) \forall i$
2. Same slope: $S'_{i-1,i}(x_i) = S'_{i,i+1}(x_i) \forall i$
3. Same concavity: $S''_{i-1,i}(x_i) = S''_{i,i+1}(x_i) = K_i \forall i$
The polynomials can be of any order but for $k = 1$ the second and third condition aren't completely satisfied. The same goes for $k = 2$ and the third condition. Naturally, for the imposed conditions it's required $k \geq 3$, but for this specific case, we'll stick with this lowest possible order.
Therefore, for third order:
$S(x)$: piecewise cubic polynomial.
$S'(x)$: piecewise quadratic polynomial.
$S''(x)$: piecewise lineal polynomial.
Since no information is known related to $S(x)$, one starts by putting forward a Lagrange interpolation for the second derivative:
$$S''_{i,i+1}(x) = K_i \frac{x-x_{i+1}}{x_i - x_{i+1}} + K_{i+1} \frac{x-x_{i}}{x_{i+1} - x_i}$$
Integrating twice: $$S_{i,i+1}(x) = \frac{K_i}{6} \frac{(x-x_{i+1})^3}{x_i-x_{i+1}} + \frac{K_{i+1}}{6} \frac{(x-x_i)^3}{x_{i+1}-x_i} + C_1x + C_2$$ Redefining the constants $C_1 = \alpha - \beta$ and $C_2 = -\alpha x_{i+1} + \beta x_i$ and giving it a more symmetric structure: $$S_{i,i+1}(x) = \frac{K_i}{6} \frac{(x-x_{i+1})^3}{x_i-x_{i+1}} + \frac{K_{i+1}}{6} \frac{(x-x_i)^3}{x_{i+1}-x_i} + \alpha (x-x_{i+1}) + \beta (x-x_i)$$
Given that $S_{i,i+1}(x_i) = y_i \Rightarrow \alpha = \frac{y_i}{x_i-x_{i+1}} - \frac{K_i}{6}(x_i-x_{i+1})$
Given that $S_{i,i+1}(x_{i+1}) = y_{i+1} \Rightarrow \beta = \frac{y_{i+1}}{x_{i+1}-x_i} - \frac{K_{i+1}}{6}(x_{i+1}-x_i)$
This is function will be able to interpolate the data once the values $K_i, K_{i+1}$ are known. \begin{align} \begin{split} S_{i,i+1}(x) = \frac{K_i}{6} (\frac{(x-x_{i+1})^3}{x_i-x_{i+1}} -(x-x_{i+1})(x_i-x_{i+1})) - \frac{K_{i+1}}{6} (\frac{(x-x_i)^3}{x_i-x_{i+1}} \\ \quad - (x-x_i)(x_i-x_{i+1})) + \frac{y_i(x-x_{i+1})-y_{i+1}(x-x_i)}{x_i-x_{i+1}} \end{split} \end{align} Requiring the spline to have continuous first derivatives $S'_{i-1,i}(x_i) = S'_{i,i+1}(x_i)$ (2nd condition previously mentioned) one finds the relation: \begin{align} \begin{split} K_{i+1}(x_{i}-x_{i+1})+2K_i(x_{i-1}-x_{i+1})+K_{i-1}(x_{i-1}-x_{i}) \\ \quad = 6(\frac{y_{i+1}-y_i}{x_{i+1}-x_i}-\frac{y_i-y_{i-1}}{x_i-x_{i-1}}) \end{split} \end{align} where the right hand side is proportional to the difference of the slopes. By solving this system of $N$ linear equations, one finds the values of all the $K_i$ elements. This has been programmed using Julia 1.4.0, where the Plots and LinearAlgebra libraries have been used and can be obtained from [my personal github repository.](https://github.com/omaraalvarez/CubicSplineInterpolation)
This spline must satisfy three basic conditions:
1. Continous function: $S_{i-1,i}(x_i) = S_{i,i+1}(x_i) \forall i$
2. Same slope: $S'_{i-1,i}(x_i) = S'_{i,i+1}(x_i) \forall i$
3. Same concavity: $S''_{i-1,i}(x_i) = S''_{i,i+1}(x_i) = K_i \forall i$
The polynomials can be of any order but for $k = 1$ the second and third condition aren't completely satisfied. The same goes for $k = 2$ and the third condition. Naturally, for the imposed conditions it's required $k \geq 3$, but for this specific case, we'll stick with this lowest possible order.
Therefore, for third order:
$S(x)$: piecewise cubic polynomial.
$S'(x)$: piecewise quadratic polynomial.
$S''(x)$: piecewise lineal polynomial.
Since no information is known related to $S(x)$, one starts by putting forward a Lagrange interpolation for the second derivative:
$$S''_{i,i+1}(x) = K_i \frac{x-x_{i+1}}{x_i - x_{i+1}} + K_{i+1} \frac{x-x_{i}}{x_{i+1} - x_i}$$
Integrating twice: $$S_{i,i+1}(x) = \frac{K_i}{6} \frac{(x-x_{i+1})^3}{x_i-x_{i+1}} + \frac{K_{i+1}}{6} \frac{(x-x_i)^3}{x_{i+1}-x_i} + C_1x + C_2$$ Redefining the constants $C_1 = \alpha - \beta$ and $C_2 = -\alpha x_{i+1} + \beta x_i$ and giving it a more symmetric structure: $$S_{i,i+1}(x) = \frac{K_i}{6} \frac{(x-x_{i+1})^3}{x_i-x_{i+1}} + \frac{K_{i+1}}{6} \frac{(x-x_i)^3}{x_{i+1}-x_i} + \alpha (x-x_{i+1}) + \beta (x-x_i)$$
Given that $S_{i,i+1}(x_i) = y_i \Rightarrow \alpha = \frac{y_i}{x_i-x_{i+1}} - \frac{K_i}{6}(x_i-x_{i+1})$
Given that $S_{i,i+1}(x_{i+1}) = y_{i+1} \Rightarrow \beta = \frac{y_{i+1}}{x_{i+1}-x_i} - \frac{K_{i+1}}{6}(x_{i+1}-x_i)$
This is function will be able to interpolate the data once the values $K_i, K_{i+1}$ are known. \begin{align} \begin{split} S_{i,i+1}(x) = \frac{K_i}{6} (\frac{(x-x_{i+1})^3}{x_i-x_{i+1}} -(x-x_{i+1})(x_i-x_{i+1})) - \frac{K_{i+1}}{6} (\frac{(x-x_i)^3}{x_i-x_{i+1}} \\ \quad - (x-x_i)(x_i-x_{i+1})) + \frac{y_i(x-x_{i+1})-y_{i+1}(x-x_i)}{x_i-x_{i+1}} \end{split} \end{align} Requiring the spline to have continuous first derivatives $S'_{i-1,i}(x_i) = S'_{i,i+1}(x_i)$ (2nd condition previously mentioned) one finds the relation: \begin{align} \begin{split} K_{i+1}(x_{i}-x_{i+1})+2K_i(x_{i-1}-x_{i+1})+K_{i-1}(x_{i-1}-x_{i}) \\ \quad = 6(\frac{y_{i+1}-y_i}{x_{i+1}-x_i}-\frac{y_i-y_{i-1}}{x_i-x_{i-1}}) \end{split} \end{align} where the right hand side is proportional to the difference of the slopes. By solving this system of $N$ linear equations, one finds the values of all the $K_i$ elements. This has been programmed using Julia 1.4.0, where the Plots and LinearAlgebra libraries have been used and can be obtained from [my personal github repository.](https://github.com/omaraalvarez/CubicSplineInterpolation)